Grafuri euleriene
Fie G=(V, E) un graf neorientat,
unde V are n elemente (n noduri) si E are m elemente (m muchii).
Lanț eulerian = un lanț simplu care conține toate muchiile unui
graf
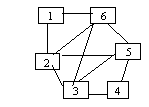
Lantul: L=[1.2.3.4.5.3.6.2.5.6] este lant
eulerian
Ciclu eulerian = un ciclu simplu care conține toate muchiile grafului
Ciclul:
C=[1.2.3.4.5.3.6.2.5.6.1] este ciclu eulerian
Graf eulerian = un graf care
conține un ciclu eulerian.
Condiție
necesară și suficientă: Un graf este eulerian dacă și numai dacă oricare vârf
al său are gradul par.
Observatie: graful poate fi eulerian si daca
contine noduri izolate.
Problema: fiind dat un graf fara noduri izolate
sa se determine daca este eulerian. In caz afirmativ se vor afisa toate
ciclurile euleriene care incep cu un nod nd citit.
-
vom determina daca graful este conex
-
vom determina daca fiecare nod are grad par
-
vom genera toate ciclurile euleriene utilizand tehnica
backtracking. Astfel:
o
primul nod va trebui sa fie nd
o
un nou x=st[k], adaugat in stiva trebuie sa fie
adiacent cu anteriorul (y=st[k-1])
o
muchia x-y nu trebuie sa mai fi fost adaugata inca odata
o
ultimul nod, care incheie ciclul, trebuie sa fie incident
cu primul
O solutie:
#include<fstream;
using namespace std;
int st[100];
int k,nd;
int a[10][10],viz[10],n,m;
void df_r(int nod) //parcurgere in adancime
{int k;
cout<<nod<<" ";
viz[nod]=1;
for(k=1;k<=n;k++)
if(a[nod][k]&&!viz[k])
df_r(k);
}
int e_valid()
{int x,y;
if(k==1)
if(st[k]!=nd)
return 0;
if(k>1) //sa existe muchie cu precedentul
{x=st[k];
y=st[k-1];
if(a[x][y]==0)
return 0;
}
for(int i=1;i<=k-2;i++)
if((st[i]==x && st[i+1]==y) || (st[i]==y && st[i+1]==x))
return 0; //muchia a mai fost luata odata
//ultima muchie sa
fie incidenta cu prima
if(k==m)
if(a[st[m]][st[1]]==0)
return 0;
return 1;}
void tipar()
{for(int i=1;i<=m;i++)
cout<<st[i]<<" ";
cout<<st[1];
cout<<endl;
}
void back()
{ k=1;
while(k>0)
{if(st[k]<n)
{st[k]++;
if(e_valid())
if(k==m)
tipar();
else{k++;
st[k]=0;
}
}
else
k--;}
}
int main()
{int x,y;
fstream f;//int a[10][10];// citire matrice din fisier
f.open("matsim.txt",ios::in);
if(f)
cout<<"ok";
else
cout<<"error";
f>>n>>m;
for(int i=1;i<=m;i++)
{f>>x>>y;
a[x][y]=a[y][x]=1;
}
cout<<"matricea
de adiac "<<endl; // afisare matrice
for( i=1;i<=n;i++)
{for(int j=1;j<=m;j++)
cout<<a[i][j]<<" ";
cout<<endl;
}
cout<<"nd="; //nodul de la care se porneste
cin>>nd;
df_r(nd);
int s=0;
for(i=1;i<=n;i++)
s+=viz[i];
//pentru a verifica daca graful este conex
if(s!=n)
cout<<"graful nu e conex ";
else
{int gasit=0;
cout<<endl<<"graful e
conex!"<<endl;
for(i=1;i<=n;i++) //determin daca toate nodurile au gradele pare
{s=0;
for (int
j=1;j<=n;j++)
s+=a[i][j];
if(s%2!=0)
gasit=1;}
if(gasit)
cout<<"am noduri fara grade pare";
else
cout<<"toate nodurile au
gradele pare deci graful e eulerian";
}
back();
return 0;
}
O varianta mai eficienta de determinare a unui
ciclu eulerian este urmatoarea:
Fie graful din figura urmatoare:
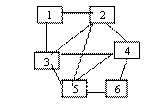
-se determina daca graful contine un ciclu
eulerian (toate nodurile au grad par si este conex)
-se retin gradele tuturor nodurilor in vectorul
g. Acesta va retine:
g=[2,4,4,4,4,2]
-ciclul se genereaza pas cu pas retinand nodurile
intr-o lista gestionata de variabilele p si u (prima si ultima componenta)
-se genereaza un ciclu pornind de la nodul 1 care
se adauga in lista p (acesta va fi si u la inceput). In continuare se adauga
noduri adiacente cu informatia retinuta de u si se continua astfel pana se
ajunge iar la nodul 1. De fiecare data cand se adauga o muchie (u->info, i)
la ciclu se micsoreaza gradul lui
u->info si lui i iar muchiile (u->info, i) si (i,u->info) se
elimina.
-acest prim ciclu se poate genera parcurgand
nodurile grafului
-dupa prima secventa se determina ciclul :
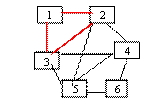
-
lista va retine : p={1, 2, 3, 1} iar g devine : g=[0, 2, 2, 4, 4, 2]
-
in continuare se cauta un nou ciclu care sa porneasca de
la un nod x din p si pt care g[x]>0. Primul astfel de nod gasit este : x=2.
Acest nou ciclu este memorat de o noua lista gestinata de p1 si u1. Ciclul nou se cauta
dupa acelasi principiu. Se obtine :
p1={2, 4, 3, 5, 2} iar g
devine : g=[0,0,0,1,1,1]
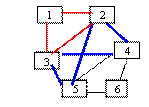
Noul ciclu se insereaza dupa x gasit (x=2, se insereaza lista p1 in lista
p) si se obtine : p={1,2,4,3,5,2,3,1}
-mai departe pe acelasi principiu se cauta x (x=4)iar urmatorul ciclu este
p1={4, 5,6,4} si g ajunge la g={0,0,0,0,0,0}. Acesta se insereaza dupa 4 :
Se obtine : p={1,2,4,5,6,4,3,5,2,3,1}
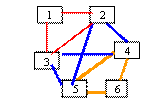
O variabila k retine numarul muchiilor adaugate la ciclu si algoritmul
continua pana k ajunge la m (numarul de muchii).
O solutie de implementare este :
#include<fstream>
using namespace std;
struct nod{int info;
nod *next;};
int a[20][20],viz[20];
int g[20];
int n,m,k;
void df(int nod)
{viz[nod]=1;
for(int k=1;k<=n;k++)
if(a[nod][k]==1&&viz[k]==0)
df(k);
}
void citire()
{ int x,y;
fstream f; //memorare graf in matrice de adiacenta
f.open("euler.txt",ios::in);
if(f)
cout<<"ok";
else
cout<<"eroare";
cout<<endl;
f>>n>>m;
for(int i=1;i<=m;i++)
{f>>x>>y;
g[x]++; g[y]++;
a[x][y]=a[y][x]=1;
}
}
int verific()
{ for(int i=1;i<=n;i++)
if(g[i]%2==1)
return 0;
df(1);
for(i=1;i<=n;i++)
if(viz[i]==0)
return 0;
return 1;
}
void generezc1(nod*&p,nod*&u,int x)
{nod *q;
q=new nod;
q->info=x;
p=u=q;
do
{ int gas=0;
for(int
i=1;i<=n&&!gas;i++)
if(a[i][u->info]==1)
{g[u->info]--;
g[i]--;
k++;
a[i][u->info]=a[u->info][i]=0;
q=new nod;
q->info=i;
u->next=q;
u=q;
gas=1;}
}
while(p->info!=u->info);
u->next=0;
}
void afisare(nod *q)
{while(q)
{cout<<q->info<<" ";
q=q->next;}
}
int cauta(nod *&q)
{
while(q)
{if(g[q->info])
return q->info;
q=q->next;
}
return 0;
}
int main()
{
citire();
if(verific()==0)
cout<<"gf nu este
eulerian!";
else
{ cout<<"este
eulerian!";
nod *p=0,*u;
cout<<endl;
generezc1(p,u,1);
cout<<endl;
nod *p1=0,*u1;
while(k<m)
{nod *q=p;
int x=cauta(q);
generezc1(p1,u1,x);
u1->next=q->next;
q->next=p1->next;
}
afisare(p); }
return 0;
}